The Graphic-Analytical Method.
The graphic-analytical method (GAM), developed by the author, was used in studies of prehistoric ethnogenetic processes and its effectiveness has been proved by the obtained results, which are confirmed by other studies. The author came to the idea of a possible mathematical evaluation of the degree of kinship between the languages of one family or group after becoming acquainted with works of linguists of the distant past. The first view of language kinship was formed under the influence of the thoughts of Herman Paul:
We must admit, strictly speaking, that there are as many separate languages in the world as there are individuals… If the intensity of communication would be uniform in all points of a given language territory, then individual languages, where they are closely related, would generate only minor deviations, while at the opposite ends of the territory there were still sharp discrepancies. Then it would be impossible to single out any group of individual languages in order to oppose it as closed integrity to another such group. The language of each individual could then be considered as a transitional step to the languages of many other individuals. This position, however, never existed anywhere. It would be possible if there were neither natural borders nor political and religious associations, if, say, all the people lived on a single plain, not crossed by any significant river, in isolated farms located at the same distance from each other, without common gathering places. However, even in this case, there would be a process of language unification, at least in the languages of individual families [PAUL H. 1960, 58, 61.]
The method was developed in the early eighties of the last century and was described for the first time in 1987 in the article "The Determination of Habitats of Ancient Slavs by a Graphic-Analytical Method" in the magazine "Proceedings of the Academy of Sciences of the USSR. The Series of Literature and Language. Volume LXIV:1, Moscow" (in Russian). GAM is the practical implementation of the theoretical reasoning of a Ukrainian philologist Illarion Swiencyckyi who, defending the need for the application of mathematics in the humanities, wrote:
It is important only that all sorts of human and world relationships are easiest to denote by numbers, volume, and position in space and time, as they can easily fit into the framework of mathematical symbols [SWIENCYCKYI I., 1927, 53]
The graphic-analytical method, indeed, determines the relative position of related languages in space at a certain time what allows us to investigate the origin and development of languages in the prehistoric period. The idea of the method consists of the geometrical interpretation of interrelations of related languages on the basis of a quantitative evaluation of mutual linguistic units in pairs of languages of one language family or group. A greater affinity of languages is usually associated with a large number of mutual linguistic units, of which words are most suitable for statistical processing. A large number of words allows you to avoid excessive values of distinct language units for the evaluation of kinship when their number is small. The starting point in the development of the method was the assumption of the existence of an inverse relationship between the number of mutual words in a pair of languages and the distance between the areas in which these languages were formed. Simply put, the closer the speakers of two related languages dwelled to each other, the more mutual words are present in their languages. It is clear that the words have to be ancient, such that a man could use even in prehistoric times, and not those words that arose later on the higher steps of social development. Segregating words of ancient origin is not easy, but in reality, there are various methods for this.
Let us try to substantiate the made assumption mathematically. Guided by the conclusions of Hermann Paul, we can assume that when some people settle on a vast and plain territory with no special geographical obstacles during the process of its cultural formation, at some point the increase of vocabulary connected with these advances will eventuate in the development of isolated dialects from the original unitary language of this people. And these dialects will produce such a language continuum that will result in the differences between isolated dialects that increase monotonously and proportional to the distance separating certain ethnical groups as speakers of these dialects.
Contrary to Paul’s assertion almost ideal conditions for such language development, according to the described scenario, existed in plain Australia which is not crossed by big rivers. A Russian scholar V.A. Shnirelman describes the language situation in Australia:
Language continuum was characteristic for Australian aborigines, i.e. tongues or dialects of adjacent groups demonstrated large similarity and their speakers understood each other well, whereas mutual intelligibility gradually disappeared with the distance between the groups [SHNIRELMAN V.A. 1982: 88).
If we graphically reflect the described language situation in our hypothetical territory of Australian type, it has the appearance of the line MS on Figure 1.
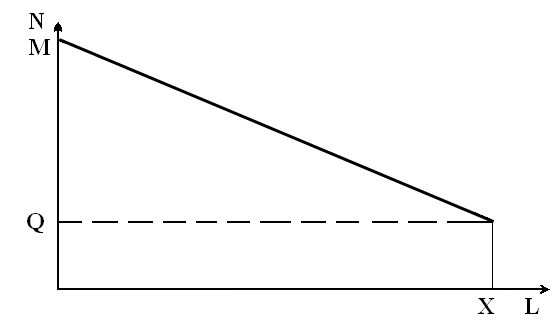
Fig.1 Distribution of the number of mutual words between the dialects on the space without geographical boundaries
N is the number of mutual words between dialects. L is the distance between the habitats. M is the total number of words in one of the dialects. Q is the number of first-level words for all dialects. X – the distance at which the community of newly formed words disappears.
If primary people had their languages with the total number of lexical items – Q from the outset of its settlement at a certain territory, the new dialects continuum could develop in two ways:
1. by the production and interchange of new words among the dialects with the increase of Q in the language,
2. by the decrease of initial total Q in each dialect.
But both processes develop at different speeds. The process of the producing and interchange of new words develops quicker than the loss of some words in the initial total vocabulary. As a result, the entire vocabulary stock of each dialect can be divided into two layers – words derived from the parent language which we name as the words of the first level, and new words which we name as the words of the second level.
It is important to clarify this above-postulated correlation of the mutual words volume and the distance between the dialects, is, in fact, influenced only by the words of the second level, because the words of the first level remain in approximately equal quantity at each time point in all the dialects.
Since the relationship between dialects is invariant, that is, the number of mutual words of the second level in them depends only on the distance between them and does not depend on their location relative to other dialects, the relationship between the number of mutual words of the second level in dialects and the distance between settlements of their carriers will be linear and expressed by the function
N = (M – Q) – kL,
where k is the coefficient of proportionality, depending on the population density, the number of dialect groups, and other factors.
If the habitat of the speakers of a distinct language has geographical barriers which prevent their equable movement and communication and causes the formation of more or less permanent settlement areas of these groups, then not a continuum of dialects but a certain number of discrete dialects arise within these habitats, boundaries between them are these geographical barriers. The size of these areas, in which on linguistic and cultural innovations emerge and spread, can not be too large, otherwise within its boundaries may occur a continuum of language that will not conduce to the consolidation of the population into a single ethnic unit.
A consequence of the existence of natural boundaries is that the language continuum on the common settlement territory is violated, and the function N = (M – Q) – kL has a discontinuity at the point of intersection of the boundary. Simply put, the number of mutual language features (among them words) between different groups within the habitat decreases monotonically in proportion to the distance between their settlements (but at a slower rate than in the type of Australia, as within the habitat of the population now has closer contacts), and the number of mutual features decreases abruptly at the border. We can assume that a certain more or less constant percentage of the mutual words of the second level is being lost at every crossing of the boundary. In this case, the distribution of the number of mutual words, depending on the distance will be like that shown in Figure 2 by the broken line MTUVWXYZ.
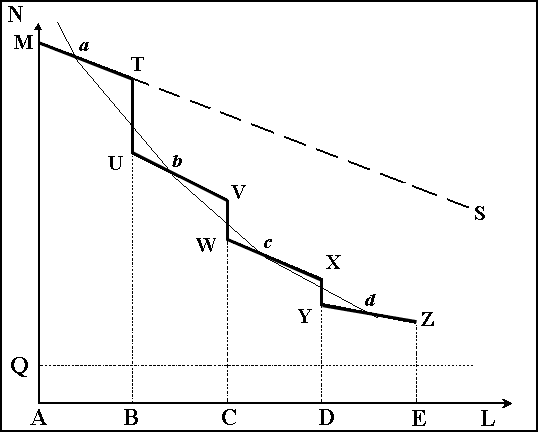
Fig. 2. Distribution of the number of mutual lexical items between dialects in areas, separated by ethnical boundaries.
N – the number of mutual lexical items in dialects; L – the distance between the habitats (areas); Q – the number of first levels lexical items, being the same for all dialects; M – the total number of words in an isolated dialect; AB, BC, CD, DE, – habitats of distinct dialects.
This distribution has too complex a mathematical expression. But if we agree to consider newly developed isolated dialects within areas AB, BC, CD, and DE as individual language units, we can consider the distance between them to be equal to the distance between their area centers. Thus, connecting the centers of segments MT, UV, WX, YZ, we obtain the distribution of mutual lexical items (words, for simplicity) in dialects as the line abcd. And if we move the origin of the coordinate to the point Q, we’ll see that the shape of this line in its central part will be close to the hyperbola; therefore it can be described with the function of inverse proportionality y=k/x. In this case, the correlation between the number of words of the second level in the dialects and the distance between the centers of habitats can be approximately described with the formula:
M – Q = K/L,
where K is the coefficient of proportionality.
Certain inaccessibility of habitats of isolated dialect speakers will eventuate in the such difference between these dialects that the parent unitary language will split into new distinct languages which we shall call further the languages of the second level. These languages can be derived again and produce new languages of the third level if the second-level language speakers migrate to a new large territory. The combined complex of words of the first and second levels will remain in the languages of the third level. This process can continue further in producing the family tree of monophyletic languages.
As the result of this process a great deal of the word complex of low levels was conserved in the languages of the higher levels, but only words of the highest level will be subordinate to the law of inverse proportionality, i. e. when the number of mutual words of this level is depended on the distance between the ethno-generating areas of languages. Thus when we analyze languages of the higher levels, we have to remove all the words of lower levels from the study, as a rule, such words are common for all analyzed languages, and it considerably facilitates their exclusion.
Based on such considerations, the idea arose of representing related languages as a graphical model for which good correspondence can be found on the surface of the Earth. Experience has shown that such a place may be the only one. To build a model, a special type of graph is used that maybe still await its description in mathematics (the author has not found it in graph theory). So far, it can be characterized as a “weighted” graph, in which links exist not between distinct nodes, but necessarily between them all, and not only the link itself is important, but also its intensity, reflected by the distance between each of the nodes. In our case, the length of the edge of the graph corresponds to the number of mutual words in a pair of languages. However, the exact number of such words is unknown to us, since it is impossible to find them all in the dictionaries. To construct a graph, it is necessary to find the close-to-reality coordinates of the nodes based on inaccurate data on the length of the edges that connect them. In principle, the construction of a graph is possible if the length of the edges is not very distorted, but the nodes already look not as distinct points, but as a set of compact points. The more compactly the points within the set are located, and the further these sets are located one from another, the more accurately the graph is constructed.
When speaking of "mutual (common) words" in the study of the kinship of languages, we mean words belonging to a certain etymological complex that have both phonetical and semantical similarities.
For the convenience of counting mutual words, two types of dictionaries were used. Initially, a semantic dictionary was compiled, in which a set of headwords was placed in a column and correspondences from the analyzed languages were given for each semantic unit. Then, the obtained synonymous nests were analyzed for phonetic similarity, which made it possible to isolate from them etymological complexes, which included words to a certain extent similar. The second type was a matrix, in one of the vertical columns of which there was a set of identifiers for the etymological complexes found. The correspondences for them were placed in horizontal lines, also forming columns for each of the languages. When matches were present in all or almost all languages, this etymological complex was excluded from the calculations since it was a common unit of the parent language that could arise elsewhere and at another time. The etymological table-dictionaries for different language families and groups developed in this way ensured an easy calculation of the number of mutual words in language pairs necessary for constructing graphs or, in other words, graphical models of language relationships within language families or groups. When the number has been calculated, you can determine the set of edges needed to build a graphical model.
The graphic-analytical method was used to study the kinship of Nostratic, Indo-European, Finno-Ugric, Turkic, Iranian, Germanic, Slavic, Sino-Tibetan, Mongolian, and Tungus-Manchu languages. The lexical material to fill in the etymological tables-dictionaries of languages belonging to the Nostratic macro-family was mainly taken from the etymological dictionaries [ABAYEV V.I. 1958-1989.; ACHARRJAN Hr. 1971.; ALATYRIEV V.I. 1988.; BEZLAJ FRANCE. 1976.; BOISAQ E. 1923.; BRÜKNER ALEKSANDER. 1957.; CLAUSON GERARD, Sir. 1972. ; EDELMAN D.I. 2011.; FRAENKEL E. 1955-1965. ; FRISK H. 1970.; HÄKKINEN KAISA. 2007.; HOLTHAUSEN F. 1934.; HOLTHAUSEN F. 1974.; HÜBSCHMANN HEINRICH. 1972.; KLUGE FRIEDRICH, SEEBOLD ELMAR. 1989.; KOPEČNÝ FRANTIŠEK. 1981.; KORNILOV G.E. 1973.; LYTKIN V.I., GULIAYEV E.S. 1970.; MACHEK V. 1957.; MARTYNAЎ V.V. 1978.; MELNYCHUK O.S. (Ed.) 1982-2006.; MEYER-LÜBKE W. 1992.; MORGENSTIERNE GEORG VALENTIN. 1927.; NADZHIP E.N. 1979.; POKORNY J. 1949-1959.; RASTORGUYEVA V.S.; SCHUSTER-SCHEWC H. 1976.; SEVORTIAN E.V. 1974.; SŁAWSKI F. 1974.; TÓTH ALFRĖD. 2007.; TRUBACHIOV O.N. (Ed.) 1974.; VASMER M. 1964-1973; VEEN P.A.F. van, SIJS NICOLINE van der, 1997; WALDE ALOIS, HOFMANN J.B., BERGER ELSBETH. 1965; YEGOROV V.G. 1964; ZAICZ GÁBOR. 2006]. However, very often, not all correspondences to the headword are given in etymological dictionaries. Therefore, additional material was taken from many other dictionaries, both dual-language and thematic. It is not necessary to have perfect command of all these analyzed languages when working with them, but it is indispensable to know their phonological peculiarities according to the requirements of comparative-historical linguistics [MEILLET A, 1938; MEILLET A., 1954; FORTUNATOV F.F.,1956; GAMKRELIDZE T.V., IVANOV V.V., 1984]. The work of H. Krahe [KRAHE HANS, 1966] was used while selecting and systematizing words of the Indo-European languages. The phonetic rules of the Finno-Ugric languages were drawn from the book of Russian linguists Lytkin V.I. and Gulajev E.S. [LYTKIN V. I., GULAYEV E.S., 1970]. and the phonetic rules of the Turkic languages were drawn from Baskakov’s classification [BASKAKOV N.A., 1960]. Etymological database was used for building kinship models of Sino-Tibetan, Mongolic, and Tungus-Manchu languages. Compiled for calculations Etymological dictionaries-tables are constantly being corrected and updated, what allows us to build more and more advanced graphical models of language relatedness.
It should be especially emphasized that GAM is effective only when processing absolute values or related to one common. Assigning the number of mutual features between two objects to their total number in these languages or in one of them cannot sufficiently characterize these two objects, since the total number of attributes of any of the objects depends on the location of the object among the others. Marginal objects have a smaller total number of features characteristic of this association, and this already characterizes their peripheral position. When we take this reduced value in the denominator, it artificially increases the ratio to us. This does not mean that marginal objects generally have fewer features. They may even have more of them, but their part may already be common not with the objects of the association under study, but with the neighboring one.
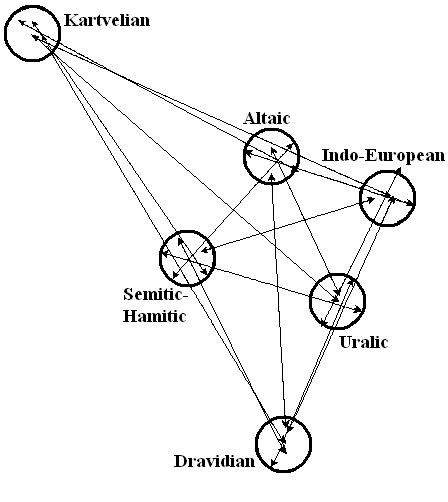
The construction of the graphical models can be demonstrated in the example of the Nostratic languages. This term is used for the phylum of six large language families of the Old World: Altaic, Uralic, Dravidian, Indo-European, Kartvelian, and Semitic-Hamitic (Hamito-Semitic, or Afro-Asiatic) which seem to have a common parent language. The necessary data for the analysis were sourced from the work of the Ukrainian linguist Illich-Switych (ILLICH-SVITYCH V.M., 1971 ). He analyzed and systematized similarities in word structure, grammar, and vocabulary of the Nostratic languages and gave a large volume of such matches between these languages in his book. The scholar assumed that these similarities can be interpreted only within the theory postulating the genetic relationship of these languages i.e. that they are monophyletic and belong to one super-family (phylum) of the Nostratic languages.
Some of the results of Illich-Svitych’ study were taken from tables in his book (morphologic features and the vocabulary of 147 units) and 286 matches were found in the further text. After the comparison of this data with the research materials of another Russian scholar (ANDREYEV N.D., 1986), consistent with the results of Illich-Switych, they were supplemented with 27 words from the Uralic languages and 8 words from the Altaic languages. As a result, it is turned out that we determined 433 features in total. Thirty-four of them were common for the whole phylum and the rest was composed of 255 units from the Altaic, 255 units from the Uralic, 253 units from the Indo-European, 240 units from the Semitic-Hamitic, 189 units from the Dravidian, and 139 units from the Kartvelian languages respectively. Then the number of mutual features in language pairs was calculated. The results of the calculation are given in table 1.
Table 1. Quantity of mutual features between language families.
| Altaic – Uralic | 167 | Uralic – Kartvelian | 66 |
| Altaic – Indo-European | 153 | Indo-European – Semitic-Hamitic | 147 |
| Altaic – Semitic-Hamitic | 149 | Indo-European – Dravidian | 108 |
| Altaic – Dravidian | 109 | Indo-European – Kartvelian | 70 |
| Altaic – Kartvelian | 84 | Semitic-Hamitic – Dravidian | 110 |
| Uralic – Indo-European | 151 | Semitic-Hamitic – Kartvelian | 86 |
| Uralic – Semitic-Hamitic | 136 | Dravidian – Kartvelian | 54 |
| Uralic – Dravidian | 134 |
After analyzing the data obtained, it is impossible to immediately find any regularity in them, but it can be noted that the Altaic, Uralic, Semitic-Hamitic, and Indo-European ones have the most common words. These languages determine the appearance of the configuration of the future graph. First, you need to choose the coefficient of proportionality, and then recalculate the number of mutual features in the distance between the areas of the languages. The choice of the coefficient value is determined by the size of the sheet on which the scheme is built. According to our data, K = 1000 is appropriate. Then the distances between the ranges of individual languages will have the values presented in Table 2:
Table 2. Distances between centers of language family areas at the diagram, cm.
| Altaic – Uralic | 6.0 | Uralic – Kartvelian | 15.2 |
| Altaic – Indo-European | 6.5 | Indo-European – Semitic-Hamitic | 6.8 |
| Altaic – Semitic-Hamitic | 6.7 | Indo-European – Dravidian | 9.3 |
| Altaic – Dravidian | 9.2 | Indo-European – Kartvelian | 14.3 |
| Altaic – Kartvelian | 11.3 | Semitic-Hamitic – Dravidian | 9.1 |
| Uralic – Indo-European | 6.6 | Semitic-Hamitic – Kartvelian | 11.6 |
| Uralic – Semitic-Hamitic | 7.3 | Dravidian – Kartvelian | 18.5 |
| Uralic – Dravidian | 7.5 |
The construction of the relationship scheme is carried out in several reiterations. First, on two coordinates for each language, we find one point, which determines the approximate position of its area, but the clarification of the location of all language areas has been got in the following iterations. In principle, you can start with any language, but it is not immediately known which way the construction will go, and the scheme can go beyond the limits of the sheet. Therefore, it is most convenient to start building a pair of languages that have the most mutual features. In our case, these are Altaic and Uralic languages.
Thus, the segment AB with a length of 6 cm, which corresponds to the number of mutual features in this pair has to be arbitrarily arranged somewhere in the center of the sheet. The ends of this segment determine the location of points for the Altaic and Uralic languages (see Fig. 3). Further, on the basis of this segment points for Indo-European and Semitic-Hamitic languages are constructed. Let us begin with the Semitic-Hamitic since these languages have more mutual features with the Kartvelian and Dravidian languages than Indo-European have.
Fig. 3. The first and the second iterations during the construction of the graphical model of the Nostratic relationships.
In accordance with the number of mutual features, the point of the Semitic-Hamitic languages has to be placed at a distance of 6.7 cm from the Altaic point and at a distance of 7.4 cm from the point of the Uralic languages. There can be two such points – to the left and to the right of the base. The choice of one of these two possible points determines the final form of the scheme, which can be of two variants, mirrored in relation to each other. We select the point closer to the center and obtain three points – A, B, C. Then we look for point D for the Indo-European languages. It also may be placed on the base AB. It has to be at the distance of 6,5 cm from the point A and at the distance of 6,6 cm from the point B. The intersection of two corresponding arcs opposite to the point C gives us the point D. (It can’t be close to the point C as the Indo-European and Semitic-Hamitic languages should have considerably more mutual features). The point E for the Dravidian languages is placed on base BC because the Semitic-Hamitic and Uralic languages have the biggest number of mutual features with Dravidian. Thus this point is placed at the distance of 7,5 cm from the Uralic point and 9,1 cm from the Semitic-Hamitic point in the direction from the center of the model. Otherwise, it lies next to the Altaic point h.e. not consistent with the number of mutual features between them. Point F for the Kartvelian languages is placed the same way but on the base AC. As the first iteration is finished, we can determine the scheme of the graphic model for the Nostratic languages. The areas of these languages are to be somehow close to the points A, B, C, D, E, F.
The second iteration makes it possible to clarify and verify the correctness of the location of the areas. Theoretically, points of individual languages can be constructed on other coordinates. For example, point D was built in two coordinates, which were segments AD and BD with segment AB as the base for them. Now we can use as coordinates, say, the same segments in other combinations – with segments that correspond to the distance between the Indo-European area and Dravidian, Semitic-Hamitic, and Kartvelian areas.
Doing so, we must choose as a base a segment adjacent to those used as coordinates. Practically this is impossible to accomplish because the position of a different base until the end of the construction of the graph remains nevertheless uncertain. However, the second iteration can be easier. In Figure 5 it is already clearly seen that the centers of the ranges of Indo-European and Semitic-Hamitic languages, in accordance with the number of mutual words, should have been closer to one another. For the same reason, the range of the Kartvelian languages should be closer to Indo-European, and the center of the Dravidian range should be closer to the Semitic-Hamite, Altai, and Indo-European. Approaching the points C and D, F and D, E and C, and E and B, respectively, and putting the segment corresponding to the number of mutual words in the respective languages on the straight line joining these points, we get the graph more correct.
Now the ends of the segments are located more compactly. You can spend the third iteration in the same way, if you see that the conditional centers of the areas need to be moved again. In so doing, we can repeat two or three iterations to get the definitive graphical model of language relationship. In our case, the model of the Nostratic language relationship has the final appearance presented in Figure 4. The figure has fractal characteristics and reminds Sierpinski triangle.
The whole configuration of the aggregate of points for each language prompts us with the direction where we have to move the areas in order to place the points forming the most compact graph. In so doing, we can repeat two or three iterations to get the definitive graphical model of language relationship. In our case, the model of the Nostratic language relationship has the final appearance presented in figure 2. The figure has fractal characteristics and reminds Sierpinski triangle
Fig. 3. The model of relationship of Nostratic languages.
The construction of a graphical model of kinship using lexical-statistical data may well be automated. For this, you need to create a program for the computer. This is a task for applied mathematics, where a compilation of mathematical models of systems is common. Automatic built models would cause greater confidence, but so far none of the applied mathematicians have decided to undertake such work. Obviously, it's still not an easy task.
Using GAM eventually led to the discovery of the phenomenon ethno-producing areas. Their existence is a kind of empirical generalization, which, according to Vernadsky, "does not differ from the scientifically established fact" (VERNADSKY V.I. 2004, § 15).
Quantitative data on the vocabulary studied using GAM for forty years.
| Languages families and groups | Number of languages | Number of etymological complexes | Total number of words |
| Sino-Tibetan | 7 | 2.775 | 9.700 |
| Tungus-Manchu | 11 | 2.234 | 10.200 |
| Mongolic | 8 | 2.250 | 8.500 |
| Nostratic | 6 | 433 | 2.600 |
| Abkhaz-Adyghe | 5 | 1.800 | 4.500 |
| Nakh-Dagestanian | 27 | 1.900 | 24.000 |
| Indo-European | 14 | 2.554 | 12.381 |
| Finno-Ugric | 12 | 1.913 | 9.584 |
| Turkic | 13 | 2.558 | 19.670 |
| Germanic | 6 | 2.630 | 11.065 |
| Iranian | 11 | 1.773 | 8.249 |
| Slavic | 10 | 3.200 | 12.000 |
| Total | 130 | ≈ 26.000 | ≈ 135.000 |